External ballistics of pneumatic weapons

At one time, a cowboy philosopher expressed the "wise" idea that the shortest distance between him and the target is a bullet. He was probably thinking of an imaginary straight line connecting the muzzle of his .45 Colt to the chest (or head) of his opponent, and this straight line he associated with a bullet.

In some ways, the cowboy philosopher was almost right, considering that he figured out his relationship with the enemy at a short distance - 5 ... 10 m, and in this case, the trajectory of his bullet can be taken approximately as a straight line.

In fact, after leaving the barrel, the bullet does not fly in a straight line, but along a certain curve, which is called a ballistic trajectory. In airless space, the ballistic trajectory would be a parabola, but in the air that surrounds us, the trajectory of the bullet, when examined in detail, will be quite complex, not located in the same plane of the curve.

Such interesting sciences as external ballistics, aerodynamics, mechanics, in particular, such a powerful section as dynamics, are engaged in the study of the features of the movement of bullets, projectiles (and indeed any abandoned bodies).

When flying in the atmosphere, two main forces act on a bullet - the force of gravity and the force of air resistance, as well as a number of less significant forces, for example, the Magnus force, which in our case, i.e. for pneumatics, it often manifests itself during the flight of spherical bullets that received an unplanned rotation in the transverse direction when flying out of the barrel), aerodynamic damping (braking) forces.

The force of gravity causes a gradual decrease in the bullet, and the force of air resistance (aerodynamic force) continuously decreases the speed of the bullet and forces it to perform in general a rather complex spatial movement (which will be discussed later). The trajectory of the bullet is also influenced by such factors as meteorological conditions (pressure, humidity and air temperature, wind) and initial disturbances at the moment the bullet leaves the barrel.

The ideal trajectory (why it is ideal, will be explained later) of the bullet flight is shown in Fig. 1, with the help of which it is also quite simple to understand the terms adopted in the shooting business.

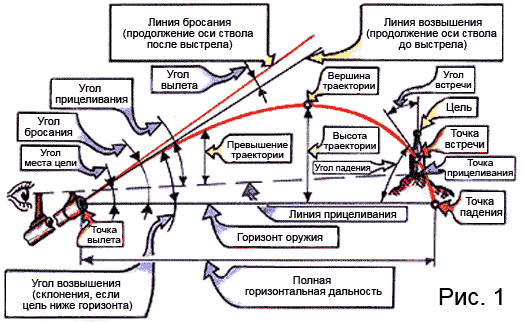
The features of the trajectory include the fact that its part from the top to the point of incidence (descending branch) is shorter and steeper than its part from the point of departure to the top (ascending branch), and the angle of incidence is greater than the angle of throw; it is obvious that the final speed of the bullet is always less than the initial one, and the flight time along the ascending branch of the trajectory, of course, is always less than along the descending one.

And now, having dealt with the terms and definitions, let us turn to Fig. 2, which shows a diagram of the main forces acting on an axisymmetric bullet (in particular, a pneumatic one) in flight. During the flight, between the longitudinal axis of the bullet and the tangent to the trajectory (the velocity vector V), there is a so-called spatial angle of attack due to the action of the initial perturbations on the bullet during the shot, wind, lowering (deflection down) of the tangent to the trajectory.

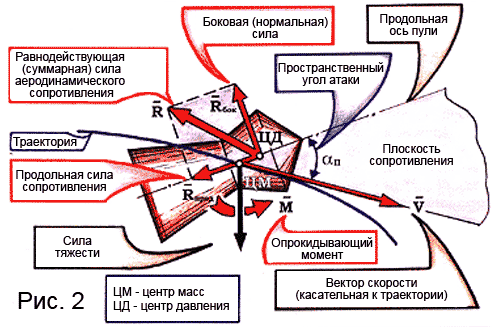
The force of gravitational attraction G is applied at the center of mass of the bullet and is directed downward. The resulting aerodynamic force R is the sum of the air pressure forces directed along the normal to the bullet surface and the air friction forces on this surface, tangential to it. The force R located in the so-called resistance plane (i.e. the plane passing through the longitudinal axis of the bullet and the velocity vector V) can be decomposed into two components. One of them is the longitudinal resistance force Rprod, located along the longitudinal axis of the bullet in the direction opposite to its top. The second is the lateral (transverse, or in relation to Fig. 2 - normal) force R side, perpendicular to the longitudinal axis of the bullet and lying in the plane of resistance.

The aerodynamic force R is applied to the bullet at a point called the center of pressure. For most pneumatic bullets, as well as for small arms and artillery shells, the center of pressure does not coincide with the center of mass of the bullet and is in front of it, i.e. closer to the top. In this case, the force R causes the aerodynamic moment M, which tends to increase the angle of attack, i.e. turn the bullet around the center of mass with its apex back (overturning aerodynamic moment).

Such a bullet is called statically (aerodynamically) unstable. Note that there are also statically stable ballistic objects in which the center of pressure is behind the center of mass, for example, darts for shooting from pneumatics, "flying" syringes-cannulas for remote injection to animals (and sometimes to people), arrows for bows, shuttlecocks for badminton and finally some cruise missiles. For these objects, the center of pressure is behind the center of mass (for this they are equipped with stabilizers - a brush, skirt, plumage, etc.), and the aerodynamic moment tends to eliminate the angle of attack that has arisen, i.e. align the longitudinal axis of the object with the velocity vector (stabilizing aerodynamic moment). It is not always possible to make statically stable bullets, and it is not always advisable for ballistic reasons.

Finally, there are objects that are statically neutral, such as a ball, which ideally has its center of pressure at its center of mass (geometric center).

So how do you ensure the movement of statically unstable bullets "head first"? to exclude their overturning under the influence of aerodynamic forces and thereby to obtain good accuracy and accuracy of fire? This can be achieved by giving the bullet a fast rotational motion around the longitudinal axis (rotation stabilization). Such rotation can be carried out both with the help of the same aerodynamic forces (for example, in turbine bullets for smooth-bore weapons), and in a more familiar way for us - with the help of special screw grooves in the barrel bore, which are used very often in pneumatic weapons, and in firearms weapons (conventional and high-precision) - all the time. For a rapidly rotating bullet, it is possible, without a large error, to assume that its angular momentum coincides with the longitudinal axis and is directed towards its top with right rotation (clockwise, when viewed from the bottom) and towards the bottom with the left. With regard to gyroscopes (and our bullet is an excellent gyroscope), such a kinetic moment is called intrinsic angular momentum (it is defined as the product of the angular velocity of rotation by the moment of inertia of the bullet relative to the longitudinal axis). And this is its own kinetic moment and "keeps" the bullet on the trajectory, preventing it from overturning.

Let us consider how this happens in the case of a bullet that flies out of the barrel "perfectly", i.e. without interference. In this case, at the beginning of the flight, the longitudinal axis of the bullet coincides with the velocity vector (with a tangent to the trajectory), i.e. the spatial angle of attack is zero. The aerodynamic force is directed along the axis of the bullet and simply slows it down. Then, under the influence of the force of gravity, the tangent to the trajectory begins to decrease, and an angle of attack appears. Aerodynamic force R continues to decelerate the bullet (force Rprod) and at the same time (force Rbok) tries to overturn it (in Fig. 2 - turn it counterclockwise around the center of mass by moment M). And since the bullet has its own kinetic moment, a compensating gyroscopic moment appears, equal to the overturning moment M, but directed in the opposite direction.

The bullet, in accordance with the properties of the gyroscope, will begin to deviate not in the direction of the action of the force, but in the direction perpendicular to the force, in this case - to the right. But as soon as the bullet tip begins to move to the right, the position of the resistance plane will begin to change, i.e. and the direction of action of the component of the aerodynamic force R side - it will also begin to act to the right. The top of the bullet will begin to go down, the force R side - also down, etc. As a result, the top of the bullet describes a circle, and its longitudinal axis is a cone with the top at the center of mass. This movement is called precessional or simply precession (Fig. 3). Since the angle of attack (half-opening of the precession cone) is small enough, the bullet flies with its top forward. But this is ideally, i.e. as it was said, for the flight of a bullet without initial interference. In fact, at the moment of departure from the barrel, due to its startle (for example, from recoil) and under the residual action of compressed gas (air), the bullet receives some lateral push or impulse. Generally speaking, the direction of this push can be arbitrary. Under these conditions, it is most natural (as is customary in shooting and artillery practice) to believe that when it leaves the barrel, a bullet from a push almost instantly acquires an initial angular velocity in the transverse direction. In this regard (and again in connection with the properties of the gyroscope), the longitudinal axis of the bullet will begin to perform additional radial motion (oscillations), called nutation or simply nutation.

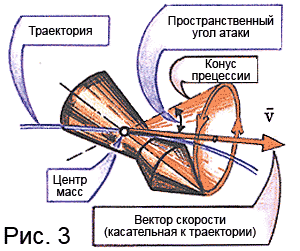
As a result (Fig. 4), the top of the bullet will begin to describe a rather tricky curve called the epicycloid, and the longitudinal axis of the bullet will be a very intricate cone with the base in the form of this very epicycloid. Nutation oscillations gradually damp under the action of aerodynamic damping forces.

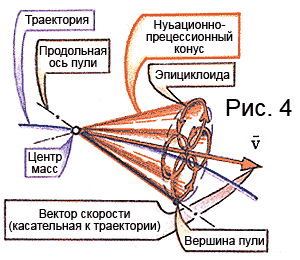
Naturally, at first glance, it seems that the mentioned cones are described by the longitudinal axis of the bullet around the velocity vector (i.e., around the tangent to the trajectory), which actually happens at the very beginning of the trajectory. But then the tangent to the trajectory under the action of the force of attraction begins to decrease, and this leads to the fact that the bullet begins to oscillate not relative to the velocity vector, but relative to the so-called dynamic equilibrium axis, which is deflected sideways (to the right with right rotation) from the velocity vector by a certain angle ... This angle, in particular, is directly proportional to the speed of rotation of the bullet and the steepness of the trajectory. And this very deviation to the right of the dynamic axis of equilibrium from the velocity vector leads to the appearance of an additional lateral "add-on" to the aerodynamic force, as a result of which there is an additional displacement of the center of mass of the bullet also to the right. This specific phenomenon is called derivation, which must be taken into account when shooting at long ranges.

Well, if you are scrupulous enough, the following should be noted. Angular precession-nutation oscillations of the bullet around the center of mass lead to the fact that the center of mass itself, simultaneously with the derivational drift, performs the same oscillations in the transverse plane, i.e. describes a gradually decaying epicycloid.

Thus, the trajectory of the bullet, as mentioned at the beginning of the article, is a really complex curve: the center of mass of the bullet flies forward and to the right (derivation), while performing transverse epicycloidal oscillations, and the bullet itself performs the same oscillations around the center of mass. However, let us, dear reader, not be confused by this: all transverse oscillations of pneumatic bullets, and mainly small arms, as will be shown below, are very, very small and, moreover, they gradually fade (these oscillations are felt in powerful long-range artillery), and the derivation is compensated by correct zeroing.

It is necessary to note the dual nature of the action of the overturning moment on the bullet from the aerodynamic force. On the one hand, this moment makes it necessary to give the bullet gyroscopic stability due to rotation in order to prevent it from tumbling (and not to worsen the range, accuracy and accuracy of fire). On the other hand, on the curved section of the trajectory, the rotating bullet "follows" the tangent to the trajectory only due to the fact that it is affected by the overturning moment. If it were not for this moment (there would be no air), the longitudinal axis of the bullet (the vector of its own angular momentum) while moving along the trajectory would move plane-parallel and would retain the initial orientation in space obtained when leaving the barrel (i.e., the bullet could would hit the target at a large angle, or even almost sideways).

We talk about the rotation of the bullet all the time, and a natural question arises, with what angular velocity to rotate it. Without getting into the dense jungle of mechanics, aerodynamics, stability theory, we note that the choice of rotation speed is carried out according to two criteria. The first criterion sets the lower value of the angular velocity that is permissible to ensure the stability of the bullet, based on the ratios of the moments of inertia of the bullet relative to the longitudinal and transverse axes, its initial velocity, cross-sectional area, the distance between the center of mass and the center of pressure (shoulder of aerodynamic force), some aerodynamic coefficients. The second criterion determines the upper limit of the rotation speed, proceeding from the minimization of the angle of deviation of the dynamic equilibrium axis from the velocity vector: a stable rotating bullet must "follow" the tangent to the trajectory, therefore, large deviations of the dynamic axis should not be allowed (that is, the rotation speed must not be excessively increased ). This boundary is determined by the steady motion of the bullet at the apex of the trajectory, i.e. at the critical point where the inflection is observed. An incident is possible here - the lower limit is superior to the upper one: this happens at very high angles of throw (more than 70 degrees), characteristic of powerful long-range artillery. In this case, you have to look for other ways to ensure the stabilization of the projectiles (for example, using the plumage).

Since we shoot from pneumatics along very flat trajectories (in most cases with throwing angles less than 10 degrees), then for us "re-stabilization" of the bullet by rotation is not terrible, especially if the target is hit on the ascending branch of the trajectory (and often it happens) ... At the same time, since for each pneumatic caliber there is a whole range of bullets with varying degrees of static instability (which is determined by the ratio of the difference between the distances from the bullet tip to the center of mass and the center of pressure to its length), the spread of mass-dimensional characteristics, etc., the company- gun makers usually produce versatile barrels with steep grooves to guarantee the stability of even the most volatile bullets. Therefore, the speed of rotation of the bullet is selected with a sufficiently large margin - 25 ... 50% more than the minimum allowable value.

The specified angular velocity of rotation of the bullet is provided by rifling in the barrel. Their stroke length is equal to the linear (muzzle) speed of the bullet, divided by the speed of rotation (angular velocity) and multiplied by 2p. If the length of the rifling stroke is divided by the caliber of the barrel, then we get the length of the rifling stroke in calibers (a more universal parameter).

It is necessary to briefly mention the influence of weather conditions on the flight of a bullet. Normal meteorological conditions are air temperature +15 C, pressure 750 mm Hg. Art., humidity 50%, no wind. Changes in weather conditions directly affect air density, i.e. and on the aerodynamic force proportional to it, which acts on the bullet.

So, an increase in atmospheric pressure, humidity and a decrease in temperature leads to an increase in air density (and, as a result, to a decrease in the range of a bullet) and vice versa. The wind affects the flight of bullets, again through the same aerodynamic force. If the wind is favorable or headwind, then the longitudinal resistance force decreases or increases accordingly, which means that the range of the bullet's flight increases or decreases.

A crosswind leads to the appearance of an additional angle of attack in the lateral plane, i.e. to an increase in the lateral component of the aerodynamic force and, accordingly, to the deflection of the bullet in the direction where the wind is blowing. With regard to pneumatics, we note that strong (speed 6 ... 8 m / s) and moderate (4 ... 5 m / s) wind significantly affects a light bullet with a low lateral load (the ratio of the mass of the bullet to its cross-sectional area ) and relatively low speed.

These are, in brief, the theoretical foundations of bullet flight. Here we deliberately do not talk about such sections of external ballistics as dispersion, sighting of weapons, etc., since they are quite fully described in the available manuals on shooting.

Let's talk a little better about the practical side of the flight of a bullet (otherwise theoretical "grains" are all fine wording, but you need to peck something).

Consider a typical 4.5 mm diablo-type pneumatic bullet with a domed head, Gamo Hunter, which has a fairly high accuracy and retains maximum energy at long ranges.

The average data for such a pool are as follows: weight ~ 0.47 g (7.25 grains); length ~ 5.7 mm; the diameter of the head part is 4.5 mm, the diameter of the skirt is 4.7 mm; the distance of the center of mass from the top is ~ 2.73 mm, and the center of pressure is ~ 2.4 mm (the bullet has a small static instability - 5.8%).

The rest of the parameters (such as, for example, the moments of inertia of a bullet, its aerodynamic coefficients) will not overload the reader, and distract him from the main thing - to see the behavior of the bullet in flight in figures.

Let the bullet be fired from a 4.5 mm Crosman 1377 reusable compression pistol with a 250 mm barrel and 500 mm right rifle stroke. The average muzzle velocity at 10 shots is about 168 m / s. The considered barrel gives the bullet an angular rotation speed of ~ 211.1 s, i.e. ~ 336 rps. The minimum required speed for such a bullet from the condition of ensuring gyroscopic stability is ~ 150.5 s (240 r / s), so that the safety factor for rotation speed for our bullet is about 1.4.

We assume that when leaving the barrel, the bullet receives initial conditions that are sufficiently rigid for pneumatics - the initial angular velocity in the transverse direction is 50 deg / s (the spread of the initial angular velocities in the transverse direction for small arms is 30 ... 60 deg / s, and in pneumatics can be even less, depending on the type of weapon, gunner attachment, etc.).

In fig. 5, based on the results of calculations, an illustration of the angular motion of the bullet tip relative to the dynamic equilibrium axis in projection onto the transverse plane is shown (the bullet flies at the observer).

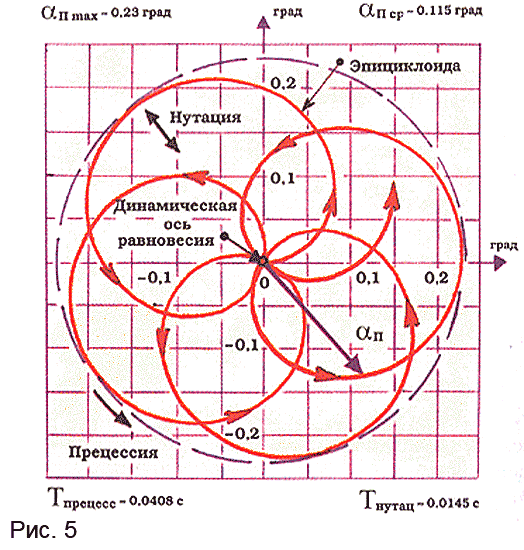
The maximum value of the spatial angle of attack for the given initial conditions is ~ 0.23 degrees, the average value is ~ 0.115 degrees, (a tiny value, almost zero!). The dynamic equilibrium axis deviates from the velocity vector by a maximum angle of 0.043 degrees, (so little that it can be assumed that the bullet oscillates around the velocity vector). In this case, the precession period is ~ 0.0408 s, and the nutation period, respectively, is ~ 0.0145 s. Thus, our (although Spanish in origin) bullet performs very fast angular oscillations along a very small epicycloid, and even rotates very quickly around the longitudinal axis. Note that the center of mass of the bullet also describes in the transverse plane a microscopic epicycloid with a maximum radius of ~ 0.05 mm (we assume that our bullet flies smoothly) and the same temporal characteristics as for angular motion. The bullet derivation when firing at 10 m is only about 1.8 mm (although there is already something to compensate for when zeroing in!). What can be said about these small values? A small bullet and everything else is small.

And now, in conclusion, we present several simple approximate relations that allow (if, of course, there is interest) "on the knee" to calculate some of the main averaged parameters of the trajectory when firing flatly with bullets of the "diablo" type of 4.5 mm caliber with a mass of 0.50 g. that by "devil" is meant a bullet with a pronounced head part of any of the known shapes (flat, domed, hemispherical or conical) and a "skirt" (with or without a notch). Learn more about the types of bullets.

                  (The article is reprinted from the magazine "Pneumatic weapons in Russia", N 3, 2003)